在数学中,排列组合是研究不同元素按照一定顺序或方式组合起来形成不同集合的学问,它广泛应用于统计学、计算机科学、物理学等多个领域,是解决实际问题的重要工具,本文将详细介绍排列组合的基本概念、计算方法及其过程,帮助读者更好地理解和应用这一数学工具。
排列组合的基本概念
-
排列(Permutation):从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,称为这n个元素的一个排列,从“ABC”中取2个元素进行排列,可以得到“AB”、“AC”和“BC”三种排列方式。
-
组合(Combination):从n个不同元素中取出m(m≤n)个元素,不考虑元素的顺序,称为这n个元素的一个组合,从“ABC”中取2个元素进行组合,可以得到“AB”、“AC”和“BC”三种组合方式,但每种方式只计算一次,不考虑顺序。
排列的计算方法及过程
排列的计算通常使用阶乘的概念,设n为集合中元素的个数,r为要取出的元素个数,则从n个元素中取出r个元素进行排列的方法数为n的r次方阶乘,记作P(n, r)或n^r。
计算过程如下:
-
定义阶乘:n的阶乘记作n!,表示所有小于等于n的正整数的乘积,即n! = n × (n-1) × ... × 3 × 2 × 1,特别地,0! = 1。
-
计算P(n, r):P(n, r) = n! / (n-r)!,这个公式的意思是,从n个元素中取出r个元素进行排列,相当于先从n个元素中任选一个作为第一个位置上的元素(有n种选择),然后从剩下的n-1个元素中任选一个作为第二个位置上的元素(有n-1种选择),依此类推,直到选出第r个元素,但这样计算会重复考虑元素的顺序,因此需要除以(n-r)!来消除重复。
-
示例:计算P(5, 3),即从5个元素中取出3个元素进行排列,首先计算5的阶乘:5! = 5 × 4 × 3 × 2 × 1 = 120;然后计算(5-3)! = 2! = 2 × 1 = 2;最后用5!除以(5-3)!得到P(5, 3) = 120 / 2 = 60,从5个元素中取出3个元素进行排列的方法有60种。
组合的计算方法及过程
组合的计算使用组合数公式C(n, r) = n! / [r!(n-r)!],这个公式表示从n个不同元素中取出r个元素的所有组合方式的数目。
计算过程如下:
-
直接使用公式:如上所述,C(n, r) = n! / [r!(n-r)!],这是最直接的计算方法,适用于大多数情况。
-
递推法(帕斯卡三角形):帕斯卡三角形是一个数学上的三角形阵列,其每一行的数字表示该行数字上方两数之和,利用帕斯卡三角形可以直接计算出C(n, r),C(n, r) = C(n-1, r-1) + C(n-1, r),这种方法在计算小规模问题时特别有效且易于记忆。
-
示例:计算C(5, 3),首先计算5的阶乘:5! = 120;然后计算3的阶乘:3! = 6;接着计算(5-3)的阶乘:(5-3)! = 2! = 2;最后用5!除以[3!(5-3)!]得到C(5, 3) = 120 / (6 × 2) = 10,从5个元素中取出3个元素进行组合的方式有10种。
应用实例及注意事项
排列组合在现实生活中有着广泛的应用,在计算机科学中,全排列问题常用于解决密码锁的解锁方式、邮件的发送顺序等;在统计学中,组合问题常用于研究不同样本的选取方式、概率计算等。
在应用排列组合时,需要注意以下几点:
- 区分排列与组合:在解决问题时首先要明确是要求排列还是组合,这直接影响到使用哪个公式进行计算。
- 理解公式含义:熟练掌握并理解排列组合公式的含义及其推导过程,有助于更准确地应用这些公式解决问题。
- 考虑顺序与无序:在应用公式时要注意是否需要考虑元素的顺序(如排列问题)或只关心是否选取了某些元素而不考虑顺序(如组合问题)。
- 简化问题:对于复杂问题,可以先尝试将其简化为更小的子问题,再利用排列组合的知识进行求解。
排列组合作为数学中的基础而重要的概念,不仅在理论上有着深厚的数学基础,而且在解决实际问题时也发挥着不可替代的作用,通过本文的介绍,我们了解了排列组合的基本概念、计算方法及其过程,并掌握了如何在实际问题中应用这些知识,希望读者能够通过学习和实践,更好地掌握这一数学工具,为解决更多复杂问题提供有力支持。







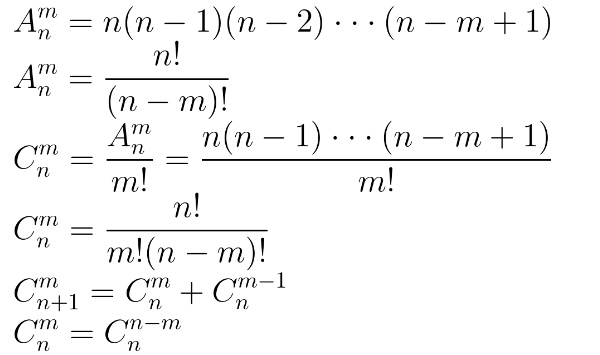
 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...